K-means clustering là một trong những thuật toán học máy không giám sát (unsupervised learning) đơn giản và phổ biến.
Thông thường, các thuật toán không giám sát đưa ra các kết luận từ các tập dữ liệu chỉ sử dụng các vectơ đầu vào mà không gắn nhãn dữ liệu hoặc giả định trước kết quả.
Mục tiêu của K-means rất đơn giản: nhóm các điểm dữ liệu tương tự lại với nhau và khám phá các cấu trúc (pattern) cơ bản. Để đạt được mục tiêu này, K-means tìm kiếm một số lượng cố định (k) các cụm trong một tập dữ liệu.
Cụm là một tập hợp các điểm dữ liệu được tập hợp lại với nhau vì có những điểm tương đồng nhất định.
Bạn sẽ xác định số mục tiêu k, là số lượng điểm trung tâm (centroid) bạn cần trong tập dữ liệu. Centroid trong toán học là trọng tâm của một hình, ví dụ trọng tâm của tam giác. Trong thuật toán K-means, Centroid là vị trí thực hoặc ảo đại diện cho trung tâm của cụm.

Nguồn: https://towardsdatascience.com/K-means-a-complete-introduction-1702af9cd8c
Mọi điểm dữ liệu được phân bổ cho từng cụm sao cho tổng bình phương khoảng cách từ các điểm dữ liệu trong cụm tới các điểm trung tâm Centroid là nhỏ nhất.
Nói cách khác, thuật toán K-means xác định k số Centroid, và sau đó phân bổ mọi điểm dữ liệu vào các cụm gần nhất, mỗi cụm tương ứng với 1 điểm trung tâm Centroid.
‘Means’ trong K-means đề cập đến điểm trung bình của dữ liệu; hay nói cách khác là tìm ra điểm trung tâm.
Cách hoạt động của thuật toán K-means
Để xử lý dữ liệu đầu vào, thuật toán K-means trong khai thác dữ liệu bắt đầu với một nhóm đầu tiên gồm các điểm trung tâm Centroid được lựa chọn ngẫu nhiên, sau đó thực hiện các phép tính lặp đi lặp lại và so sánh các giá trị tổng bình phương khoảng cách để tối ưu hóa vị trí của các điểm trung tâm này.
Thuật toán tạm dừng tạo và tối ưu hóa các cụm khi:
- Các centroid đã ổn định – không có sự thay đổi về giá trị của chúng bởi vì việc phân nhóm đã thành công.
- Đã đạt được số lần lặp (iterations) xác định.
Thực hành thuật toán K-means
Hãy xem các bước về cách hoạt động của thuật toán học máy K-means bằng cách sử dụng Kaggle Notebook.
Tôi sẽ sử dụng thư viện Scikit-learning và các dữ liệu ngẫu nhiên để minh họa giải thích đơn giản về phân cụm K-means.
Bước 1: Nhập các thư thư viện Panda, Numpy và Matplotlib:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
%matplotlib inline
Như bạn có thể thấy từ đoạn code trên, chúng ta sẽ nhập các thư viện sau vào dự án của mình:
Panda để đọc và viết bảng tính
Numpy để thực hiện các phép tính hiệu quả
Matplotlib để trực quan hóa dữ liệu
Bước 2: tạo dữ liệu ngẫu nhiên
Chúng ta sẽ nhập đoạn code sau để tạo một số dữ liệu ngẫu nhiên trong không gian 2 chiều và thể hiện các dữ liệu đó trên biểu đồ scatter plot:
X= -2 * np.random.rand(200,2)
X1 = 1 + 2 * np.random.rand(100,2)
X[100:200, :] = X1
plt.scatter(X[ : , 0], X[ :, 1], s = 50, c = 'b')
plt.show()
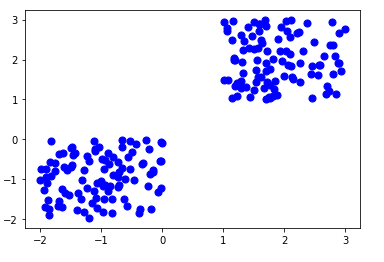
Tổng cộng 200 điểm dữ liệu đã được tạo và chia thành hai nhóm, mỗi nhóm 100 điểm.
Các dữ liệu này được hiển thị trên không gian hai chiều như sau:
Bước 3: Sử dụng Scikit-Learn
Chúng ta sẽ sử dụng chức năng K-means có sẵn trong thư viện Scikit-learning để xử lý dữ liệu ngẫu nhiên vừa được tạo ở trên.
Nhập code như sau:
from sklearn.cluster import KMeans
Kmean = KMeans(n_clusters=2)
Kmean.fit(X)
Trong trường hợp này, chúng ta đã giả định trước số cụm hay k (n_clusters) là 2.
Bước 4: Tìm centroid
Đây là code để tìm điểm trung tâm (centroid) của các cụm:
Kmean.cluster_centers_
Kết quả của giá trị của centroid trong trường hợp này là:
array([[ 1.87977152, 1.98393029], [-1.03261149, -0.92568723]])
Chúng ta có thể thể hiện các centroid này trên sơ đồ scatter plot cùng với các điểm dữ liệu ngẫu nhiên, sử dụng code như sau:
plt.scatter(X[ : , 0], X[ : , 1], s =50, c='b')
plt.scatter( 1.87977152,1.98393029, s=100, c='g', marker='s')
plt.scatter(-1.03261149, -0.92568723, s=100, c='r', marker='s')
plt.show()
Kết quả thu được:

Bước 5: Kiểm tra kết quả thuật toán
Sử dụng code như sau để lấy thuộc tính nhãn của tập dữ liệu vừa được sử dụng để phân cụm K-means; nghĩa là, cách các điểm dữ liệu được phân loại thành hai cụm.
Kmean.labels_
Kết quả:
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0], dtype=int32)
Như bạn có thể thấy ở trên, 100 điểm dữ liệu thuộc về 0 cluster trong khi phần còn lại thuộc về 1 cluster.
Tiếp theo, chẳng hạn chúng ta có một điểm dữ liệu bất kỳ, ta cần kiểm tra xem điểm dữ liệu này thuộc cụm nào. Hãy sử dụng code dưới đây:
sample_test=np.array([-3.0,-3.0])
second_test=sample_test.reshape(1, -1)
Kmean.predict(second_test)
Đây là kết quả:
array([0], dtype=int32)
Như vậy dữ liệu chúng ta vừa kiểm tra thuộc về cụm 0 (tâm màu xanh lá cây).
Kết luận
K-means clustering là một kỹ thuật được sử dụng rộng rãi để phân tích cụm dữ liệu.
Phương pháp này rất dễ hiểu và dễ thực hiện. Hơn nữa, sử dụng phương pháp phân cụm K-means cho kết quả đào tạo nhanh. Tuy nhiên, hiệu suất của nó thường không tốt bằng các kỹ thuật phân cụm phức tạp khác bởi vì các biến thể nhỏ trong dữ liệu có thể dẫn đến sai số lớn.
Hơn nữa, các cụm được giả định là hình cầu và có kích thước đồng đều, điều này có thể làm giảm độ chính xác của các kết quả phân cụm.
Trong các bài viết tiếp theo, tôi sẽ giới thiệu các phương pháp phân cụm khác nhằm khắc phục những điểm yếu của phương pháp phân cụm K-means.