K- Nearest Neighbors (kNN) là một thuật toán học máy có giám sát (supervised learning) có thể được sử dụng trong cả phân loại (classification) và hồi quy (regression). Có thể nói kNN là một thuật toán xuất phát từ thực tế cuộc sống. Mọi người có xu hướng bị ảnh hưởng bởi những người xung quanh họ. Hành vi của chúng ta được hướng dẫn bởi những người bạn mà chúng ta đã lớn lên cùng. Cha mẹ chúng ta cũng hình thành nhân cách của chúng ta theo một số cách. Nếu bạn lớn lên với những người yêu thể thao, rất có thể bạn sẽ yêu thể thao, tất nhiên cũng có những ngoại lệ.
kNN hoạt động với nguyên lý tương tự. Giá trị của một điểm dữ liệu được xác định bởi các điểm dữ liệu xung quanh nó.
Nếu bạn có một người bạn rất thân và dành phần lớn thời gian cho anh ấy / cô ấy, bạn sẽ có chung sở thích và tận hưởng những điều giống nhau. Đó là kNN với k = 1.
Nếu bạn luôn đi chơi với một nhóm 5 người, mỗi người trong nhóm có ảnh hưởng đến hành vi của bạn và bạn sẽ là trung bình của 5. Đó là kNN với k = 5.
Bộ phân loại kNN xác định lớp (class) của một điểm dữ liệu theo nguyên tắc biểu quyết đa số. Nếu k được đặt là 5, các lớp của 5 điểm gần nhất sẽ được kiểm tra. Dự đoán đưa ra kết quả lớp của điểm dữ liệu dựa vào lớp nào chiếm đa số trong 5 điểm gần nhất. Tương tự, hồi quy kNN lấy giá trị trung bình của 5 điểm gần nhất.
Làm thế nào các điểm dữ liệu được xác định là gần nhau? Trước hết cần đo khoảng cách giữa các điểm dữ liệu. Có nhiều phương pháp để đo khoảng cách. Phép đo khoảng cách Euclid là một trong những phép đo khoảng cách được sử dụng phổ biến nhất. Hình dưới đây cho thấy cách tính khoảng cách euclid giữa hai điểm trong không gian 2 chiều. Khoảng cách Euclid được tính toán bằng công thức sau:
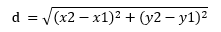

Nguồn: https://www.codespeedy.com/python-program-to-compute-euclidean-distance/
Khoảng cách Euclide trong không gian hai chiều gợi nhớ cho chúng ta định lý pythagore nổi tiếng: khoảng cách giữa 2 điểm chính là cạnh huyền của tam giác, còn chênh lệch giữa tọa độ x, y của 2 điểm dữ liệu chính là 2 cạnh góc vuông.
Sau đây tôi sẽ giới thiệu 1 ví dụ đơn giản về cách sử dụng phương pháp kNN với các dữ liệu trong không gian 2 chiều (số đặc trưng – features = 2). Tôi sử dụng Kaggle Notebook.
Đầu tiên, cần nhập các thư viện numpy, pandas, matplotib, sklearn:
import numpy as np import pandas as pd import matplotlib.pyplot as plt #datavisualization from sklearn.datasets import make_blobs #synthetic dataset from sklearn.neighbors import KNeighborsClassifier #kNN classifier from sklearn.model_selection import train_test_split #train and test sets
Scikit-learning cung cấp nhiều chức năng hữu ích để tạo bộ dữ liệu tổng hợp, rất hữu ích cho việc thực hành các thuật toán học máy. Ở đây chúng ta sẽ sử dụng hàm make_blobs.
X,y = make_blobs(n_samples = 100, n_features = 2, centers = 4, cluster_std = 1, random_state = 4)
Đoạn code này tạo ra một tập dữ liệu với 100 mẫu được chia thành 4 lớp và số đặc trưng là 2. Số lượng mẫu, số đặc trưng và lớp có thể dễ dàng được điều chỉnh bằng cách sử dụng các tham số liên quan. Chúng ta cũng có thể điều chỉnh độ phân tán (bằng cách điều chỉnh độ lệch chuẩn) của mỗi cụm (hoặc lớp). Để thể hiện tập dữ liệu tổng hợp này trên đồ thị scatter plot, chúng ta sử dụng đoạn code sau:
plt.figure(figsize = (9,6)) plt.scatter(X[:,0], X[:,1], c=y, marker = 'o', s=50) plt.show()

Đối với bất kỳ thuật toán học máy có giám sát nào, chúng ta phải chia tập dữ liệu thành các tập hợp dữ liệu đào tạo (training set) và kiểm tra (test set). Đầu tiên, chúng ta đào tạo mô hình và sau đó kiểm tra nó bằng cách sử dụng các phần khác nhau của tập dữ liệu. Nếu không thực hiện việc phân chia này, có thể chúng ta sẽ kiểm tra mô hình bằng một số dữ liệu mà nó đã biết từ trước. Việc phân chia dữ liệu này có thể được thực hiện dễ dàng bằng cách sử dụng hàm train_test_split.
X_train, X_test, y_train, y_test = train_test_split(X,y,random_state=0)
Chúng ta có thể chỉ định số lượng dữ liệu ban đầu được phân chia vào các tập dữ liệu đào tạo hoặc kiểm tra bằng cách sử dụng các tham số train_size hoặc test_size tương ứng. Tỷ lệ phân chia mặc định của hàm này là 75% cho tập dữ liệu đào tạo và 25% cho tập dữ liệu kiểm tra.
Tiếp theo, chúng ta tạo một bộ phân loại kNN. Để chỉ ra sự khác biệt giữa tầm quan trọng của giá trị k, tôi tạo hai bộ phân loại với k giá trị 1 và 5. Sau đó, các mô hình này được đào tạo bằng cách sử dụng tập hợp dữ liệu đào tạo. Trong đoạn code sau đây, tham số n_neighbors được sử dụng để chọn giá trị k. Nếu không chỉ định rõ ràng giá trị k, giá trị mặc định k=5 sẽ được sử dụng.
knn5 = KNeighborsClassifier() #k=5 knn1 = KNeighborsClassifier() #k=1 knn5.fit(X_train, y_train) knn1.fit(X_train, y_train)
Bây giờ, chúng ta sẽ dự đoán các giá trị mục tiêu trong bộ dữ liệu kiểm tra và so sánh với các giá trị thực tế.
y_pred_5 = knn5.predict(X_test) y_pred_1 = knn1.predict(X_test)
Để xem ảnh hưởng của giá trị k, chúng ta sẽ so sánh tập dữ liệu kiểm tra và các giá trị dự đoán với k = 5 và k = 1.
Dữ liệu kiểm tra gốc
plt.figure(figsize = (9,6)) plt.scatter(X_test[:,0], X_test[:,1], c=y_test, marker= 'o', s=40) plt.show()

Dữ liệu dự đoán với k=1
plt.figure(figsize = (9,6)) plt.scatter(X_test[:,0], X_test[:,1], c=y_pred_1, marker= 'o', s=40) plt.show()

Dữ liệu dự đoán với k=5
plt.figure(figsize = (9,6)) plt.scatter(X_test[:,0], X_test[:,1], c=y_pred_5, marker= 'o', s=40) plt.show()

Kết quả dường như rất giống nhau vì chúng ta đã sử dụng một tập dữ liệu có kích thước nhỏ. Nếu sử dụng tập dữ liệu có kích thước lớn hơn, chúng ta sẽ thấy có những điểm khác biệt.
Cách xác định giá trị k tối ưu
k = 1: Mô hình quá cụ thể và không khái quát hóa tốt. Nó cũng có xu hướng nhạy cảm với các dữ liệu bất thường (nhiễu) trong tập dữ liệu. Mô hình đạt được độ chính xác cao trên dữ liệu đào tạo nhưng sẽ là một công cụ dự đoán kém đối với các điểm dữ liệu mới chưa từng gặp trước đây. Do đó, chúng ta có thể sẽ tạo ra một mô hình quá khớp (overfit).
k = 100: ngược lại với trường hợp trên, mô hình quá tổng quát và không phải là một công cụ dự báo tốt trên cả tập dữ liệu đào tạo và tập dữ liệu kiểm tra. Tình trạng này được gọi là mô hình chưa khớp (underfit).
Làm thế nào để chúng ta tìm thấy giá trị k tối ưu? Scikit-learning cung cấp chức năng GridSearchCV cho phép chúng ta dễ dàng kiểm tra nhiều giá trị k khác nhau. Sau đây là một ví dụ sử dụng tập dữ liệu có sẵn trong module dataset của scikit-learning.
from sklearn.datasets import load_breast_cancer from sklearn.model_selection import GridSearchCV cancer = load_breast_cancer() (X_cancer,y_cancer) = load_breast_cancer(return_X_y = True)
Sau khi nhập các thư viện cần thiết và tải tập dữ liệu, chúng ta có thể tạo một hàm GridSearchCV như sau.
knn_grid = GridSearchCV(estimator = KNeighborsClassifier(), param_grid={'n_neighbors': np.arange(1,20)}, cv=5)
knn_grid.fit(X_cancer,y_cancer)
Ở đây, chúng ta không cần phải sử dụng hàm train_test_split để phân chia tập dữ liệu vì tham số cv sẽ thực hiện việc đó. Giá trị mặc định cho tham số cv là 5 nhưng tôi đã viết nó một cách rõ ràng để nhấn mạnh lý do tại sao chúng ta không cần sử dụng hàm train_test_split.
cv = 5 về cơ bản chia tập dữ liệu thành 5 tập con. GridSearchCV sẽ thực hiện 5 lần lặp và sử dụng 4 tập hợp con để làm dữ liệu đào tạo và 1 tập hợp con để kiểm tra tại mỗi thời điểm. Bằng cách này, chúng ta có thể sử dụng tất cả các điểm dữ liệu cho cả đào tạo và kiểm tra.
Chúng ta có thể kiểm tra giá trị k nào cho ta kết quả tốt nhất bằng cách sử dụng hàm best_params_:
knn_grid.best_params_
Kết quả:
{'n_neighbors': 13}
Trong trường hợp này, giá trị tối ưu của k là 13.
Ưu và nhược điểm của kNN
Ưu điểm
- Đơn giản và dễ giải thích
- Không dựa trên bất kỳ giả định nào, vì thế nó có thể được sử dụng trong các bài toán phi tuyến tính.
- Hoạt động tốt trong trường hợp phân loại với nhiều lớp
- Sử dụng được trong cả phân loại và hồi quy
Nhược điểm
- Trở nên rất chậm khi số lượng điểm dữ liệu tăng lên vì mô hình cần lưu trữ tất cả các điểm dữ liệu.
- Tốn bộ nhớ
- Nhạy cảm với các dữ liệu bất thường (nhiễu)